Magnetic flux is a fundamental concept in physics and electrical engineering that plays a critical role in understanding magnetic fields, electromagnetic induction, and modern technology such as generators, transformers, and MRI machines. At the core of accurately quantifying magnetic flux lies the need for a universally accepted unit of measurement. That’s where the SI unit of magnetic flux becomes essential.
The SI unit of magnetic flux allows scientists, engineers, and educators to communicate magnetic measurements consistently across various applications, from laboratory experiments to industrial design. Without a standardized unit, it would be difficult to compare results, ensure safety in electrical systems, or design efficient magnetic devices. This is why the International System of Units (SI) has assigned a specific unit to magnetic flux — the Weber (Wb).
In this article, we will explore what magnetic flux is, the significance of its SI unit, and how it is applied in the real world. We’ll also look into its mathematical formulation, derivation, historical background, and comparison with other unit systems. Whether you’re a student, engineer, or curious learner, understanding the SI unit of magnetic flux will enhance your grasp of electromagnetic principles and how they influence the devices and systems we use every day.
By the end of this guide, you’ll not only understand the definition and properties of magnetic flux but also see why the SI unit of magnetic flux — the Weber — is a cornerstone of modern electromagnetism.
1. What Is Magnetic Flux?
Magnetic flux is a measure of the total magnetic field that passes through a given area. In more technical terms, it quantifies the amount of magnetic field lines (or magnetic induction) penetrating a surface. The concept is foundational to understanding electromagnetic theory, especially when studying how magnetic fields interact with conductors to induce current, as described by Faraday’s Law.
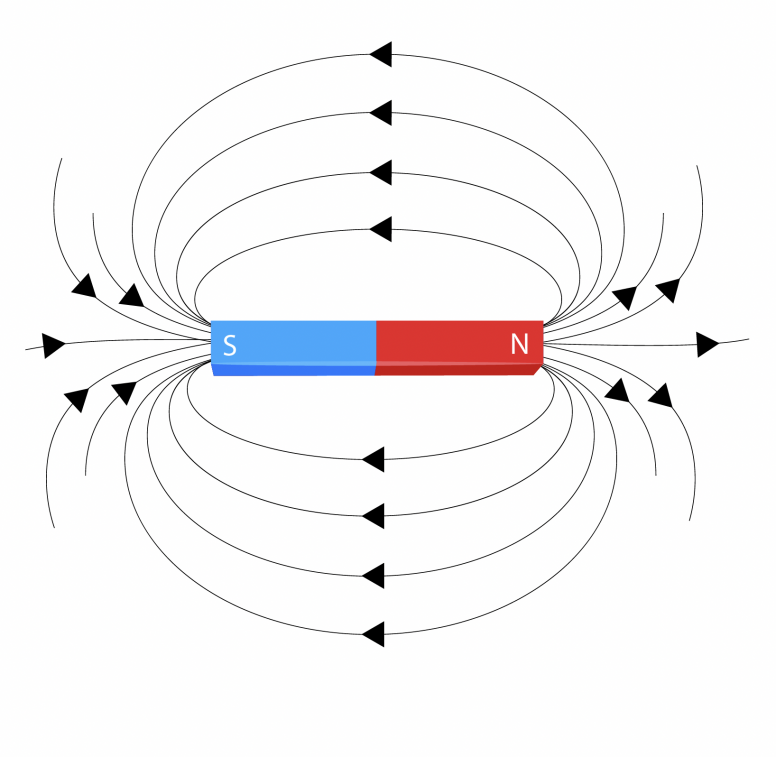
The SI unit of magnetic flux—the Weber (Wb)—helps standardize this measurement for use in equations, simulations, and practical applications across industries.
Understanding the Concept
Magnetic flux is symbolized by the Greek letter Φ (phi) or sometimes ΦB to denote magnetic flux specifically. The amount of flux depends on three key factors:
-
Magnetic field strength (B): Measured in Tesla (T)
-
Surface area (A): The area the field is passing through, in square meters (m²)
-
Angle (θ) between the field and the surface normal: Affects how much field is effectively passing through the area
The mathematical expression is:
Φ=B⋅A⋅cos(θ)
Where:
-
Φ is the magnetic flux, -
B is the magnetic field strength, -
A is the area through which the field passes, -
θ is the angle between the magnetic field and the perpendicular to the surface.
This equation shows that magnetic flux increases with stronger magnetic fields, larger surface areas, and alignment of the field perpendicular to the surface.
Physical Meaning
Imagine a flat loop of wire placed in a magnetic field. The number of magnetic field lines passing through the loop represents the magnetic flux. If you tilt the loop or change the magnetic field strength, the amount of magnetic flux changes accordingly.
This change in flux is crucial: it forms the basis of electromagnetic induction, which enables the generation of electricity in alternators and transformers. When the magnetic flux through a loop changes over time, it induces an electromotive force (EMF), which can drive an electric current.
Relevance of the SI Unit of Magnetic Flux
Since magnetic flux is used in critical equations like Faraday’s Law:
EMF=−dtdΦ
—it’s essential to have a standardized unit to ensure consistency and reliability in measurements. The SI unit of magnetic flux, the Weber, makes this possible.
In essence, magnetic flux links the magnetic field and area geometry into a single measurable quantity. Understanding what it is lays the groundwork for mastering its SI unit, applications, and how it operates in the real world.
2. The SI Unit of Magnetic Flux (Weber)
The SI unit of magnetic flux is the Weber, symbolized as Wb. This unit is integral to the International System of Units (SI) and allows for a standardized approach to measuring and expressing magnetic flux in scientific, industrial, and engineering applications.
Definition of the Weber (Wb)
One Weber is defined as the amount of magnetic flux that, linking a circuit of one turn, produces an electromotive force (EMF) of 1 volt, as the flux is reduced to zero uniformly over one second. Mathematically:
1 Wb=1 V⋅s
This definition ties magnetic flux directly to electromagnetic induction, aligning with Faraday’s Law, which states:
EMF=−dtdΦ
Where Φ is the magnetic flux. The SI unit of magnetic flux, the Weber, quantifies this rate of change in flux when EMF is induced.
SI Base Unit Derivation
To understand how the Weber is constructed from SI base units, we can break it down as:
1 Wb=1 T⋅m2
Where:
-
T (Tesla) is the SI unit of magnetic flux density
-
m² is square meters, representing area
Further expanding:
1 Wb=s2⋅Akg⋅m2
This illustrates the deep connection between the SI unit of magnetic flux and other fundamental physical quantities like mass (kg), time (s), length (m), and electric current (A).
Relation to Other Units
Here’s how the Weber connects with other units:
| Quantity | Unit | Relationship |
|---|---|---|
| Magnetic flux (Φ) | Weber (Wb) | Base SI unit of magnetic flux |
| Magnetic field (B) | Tesla (T) | 1 T = 1 Wb/m² |
| Electromotive force | Volt (V) | 1 Wb = 1 V·s |
| Flux in CGS system | Maxwell (Mx) | 1 Wb = 10⁸ Maxwells |
Thus, the SI unit of magnetic flux, the Weber, serves as the linchpin between multiple magnetic and electrical phenomena.
Historical Background of the Weber
The unit is named after Wilhelm Eduard Weber (1804–1891), a pioneering German physicist known for his contributions to magnetism and electricity. He collaborated with Carl Friedrich Gauss and played a major role in the development of the first electromagnetic telegraph.
The Weber was officially adopted as the SI unit of magnetic flux in 1946 by the International Committee for Weights and Measures (CIPM). Its formal inclusion helped unify magnetic measurements across physics, electrical engineering, and electronics.
Why the SI Unit of Magnetic Flux Matters
Without a consistent unit like the Weber, engineers and scientists would struggle to maintain accuracy and comparability in critical applications—from designing transformers and motors to modeling magnetic circuits in simulations. The SI unit of magnetic flux ensures clarity in academic papers, global standards, industrial blueprints, and technical communication.
3. Magnetic Flux in Different Unit Systems
While the SI unit of magnetic flux is the Weber (Wb), magnetic flux has also been historically measured in other unit systems, most notably the centimeter-gram-second (CGS) system. Understanding how these units compare is essential for interpreting older scientific literature, converting measurements, and working with international documentation.
Magnetic Flux in the CGS System: The Maxwell
In the CGS (Gaussian) system, the unit of magnetic flux is the Maxwell (Mx). Named after the physicist James Clerk Maxwell, one of the founders of electromagnetic theory, this unit is much smaller than the Weber.
Conversion Between SI and CGS Units:
1 Wb=108 Mx
1 Mx=10−8 Wb
This massive conversion factor highlights how much larger the Weber is compared to the Maxwell. The CGS system is still used in some niche areas of theoretical physics and older academic papers, but for all modern practical and industrial purposes, the SI unit of magnetic flux—the Weber—is the preferred standard.
Comparison Table
| Property | SI System | CGS (Gaussian) System |
|---|---|---|
| Unit Name | Weber (Wb) | Maxwell (Mx) |
| Relationship | 1 Wb = 10⁸ Mx | 1 Mx = 10⁻⁸ Wb |
| Typical Use | Modern science, engineering | Historical, theoretical physics |
| Standardization Authority | SI (BIPM, IEC, ISO) | Pre-SI, outdated usage |
Why SI Units Are the Preferred Global Standard
The SI unit of magnetic flux simplifies global communication, integration, and technology development. It fits into a broader SI framework that ensures all units—whether for length, time, mass, or electric current—are compatible and coherent.
Key reasons why the Weber is preferred over older units:
-
Ease of integration into modern formulas and systems
-
International acceptance, especially in engineering
-
Standardization in instruments, simulation software, and documentation
Real-World Implications
Using the SI unit of magnetic flux ensures consistency in:
-
International electrical codes and standards
-
Technical manuals for electric motors and transformers
-
Research papers, patents, and textbooks
-
Engineering simulations and modeling platforms (e.g., COMSOL, Ansys)
4. Understanding the Weber in Real-World Terms
The SI unit of magnetic flux, the Weber (Wb), can be difficult to visualize at first—especially since magnetic fields and flux are invisible to the naked eye. To better grasp the concept of a Weber, it’s helpful to examine practical examples and real-world analogies where this unit comes into play.
Conceptual Visualization
Let’s start with a simplified analogy:
Imagine placing a square loop of wire (1 m² in area) in a magnetic field. If the magnetic field strength is 1 Tesla and it is perpendicular to the surface of the loop, then the total magnetic flux passing through that loop is:
Φ=B⋅A=1 T⋅1 m2=1 Wb
That’s one Weber—a full measure of magnetic field lines penetrating a square meter completely aligned with the field. If the same field is at an angle, or weaker, the resulting flux will be less than one Weber.
Everyday Examples Involving Magnetic Flux
The SI unit of magnetic flux is more than a theoretical tool—it plays a major role in devices and systems we use daily, including:
1. Transformers
Transformers operate on the principle of changing magnetic flux to induce voltage in coils. The rate at which magnetic flux (in Webers) changes over time determines the induced voltage:
EMF=−dtdΦ
In power transformers, the core is often designed to guide a certain number of Webers efficiently to avoid losses and overheating.
2. Electric Motors and Generators
In motors and generators, magnetic flux links the stator and rotor. The efficiency of conversion between mechanical and electrical energy depends on the flux passing through the magnetic circuit. Too little or too much magnetic flux (measured in Webers) can reduce performance or cause damage.
3. MRI Machines
In Magnetic Resonance Imaging (MRI), powerful magnetic fields are used to align hydrogen atoms. While the magnetic field strength is measured in Teslas, the total magnetic flux through a given volume—especially when imaging large body parts—relates directly to the number of Webers passing through the area.
4. Magnetic Sensors and Hall Effect Devices
Devices like Hall Effect sensors, used in smartphones, automotive systems, and industrial automation, are designed to detect changes in magnetic flux. The SI unit of magnetic flux is used in calibrating these systems to ensure sensitivity and accuracy.
5. Wind Turbines and Energy Systems
Modern wind turbines often use permanent magnets in their generators. The magnetic flux (in Webers) produced by these magnets influences the voltage output of the generator. Engineers optimize flux paths using the SI unit of magnetic flux to maximize energy conversion.
Webers in a Quantitative Context
To further help visualize what a Weber represents:
-
A typical transformer core might carry 0.01–0.5 Webers of flux.
-
An MRI scanner can generate a magnetic field that, over several square meters, results in hundreds of Webers.
-
A compact electric motor may generate magnetic flux in the range of 0.001–0.1 Wb per pole.
Why the SI Unit of Magnetic Flux Is Critical in Design
Engineers rely on the SI unit of magnetic flux during:
-
Simulation and modeling of magnetic circuits
-
Material selection, especially in magnetic cores with specific saturation limits in Weber/m²
-
Regulatory compliance, such as ensuring safe flux densities in medical and industrial devices
Without the standardized unit—the Weber—it would be nearly impossible to design safe, efficient, and globally interoperable equipment involving magnetism.
5. Mathematical Representation and Derivation
To fully appreciate the role of the SI unit of magnetic flux, it’s important to understand how magnetic flux is mathematically defined and derived. This section explains how magnetic flux fits into key electromagnetic formulas and how the Weber connects to other SI units.
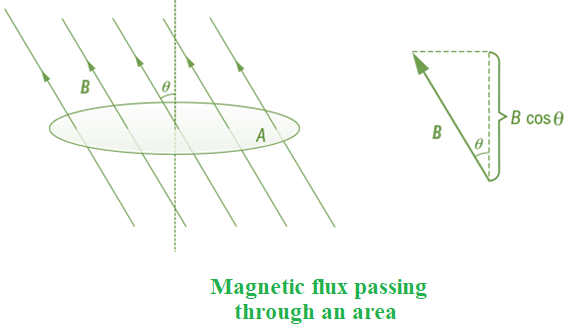
Basic Formula of Magnetic Flux
As previously introduced, magnetic flux (Φ) is calculated using the formula:
Φ=B⋅A⋅cos(θ)
Where:
-
Φ is the magnetic flux (in Webers, Wb) -
B is the magnetic flux density (in Teslas, T) -
A is the area through which the magnetic field lines pass (in square meters, m²) -
θ is the angle between the magnetic field and the normal (perpendicular) to the surface
This expression quantifies how much magnetic field “penetrates” a surface area.
Relationship with EMF: Faraday’s Law
Faraday’s Law of Electromagnetic Induction states that a change in magnetic flux over time induces an electromotive force (EMF) in a circuit:
EMF=−dtdΦ
This means the voltage (EMF) is directly related to the rate of change of magnetic flux. The unit relationship becomes:
1 Wb=1 V⋅s
So, the SI unit of magnetic flux not only describes magnetic field flow but also has a direct connection with electrical voltage and time.
Derived SI Units for the Weber
Let’s break down how the Weber is derived from other SI units:
Since
B (magnetic field strength) is measured in Tesla (T), and:
1 Tesla=1 m21 Wb
Then:
1 Wb=1 T⋅1 m2
Further decomposing the Tesla:
1 T=s2⋅Akg⇒1 Wb=s2⋅Akg⋅m2
This makes the SI unit of magnetic flux (Weber) fundamentally linked to mass, distance, time, and current — reflecting its core place in electromagnetic theory.
Worked Example
Let’s apply this in a practical scenario:
Problem:
A magnetic field of 0.3 T passes perpendicularly through a square loop of wire with an area of 0.05 m². What is the magnetic flux?
Solution:
Φ=B⋅A=0.3 T⋅0.05 m2=0.015 Wb
So the magnetic flux through the loop is 0.015 Webers, using the SI unit of magnetic flux.
Unit Consistency in Electromagnetic Formulas
The Weber ensures unit consistency across other laws and calculations, such as:
-
Lenz’s Law: Considers the direction of induced current in response to changing flux
-
Ampere’s Law and Maxwell’s Equations: Quantify the interaction between electric and magnetic fields
-
Magnetic Energy: Calculated using formulas involving magnetic flux linkage (Wb-turns)
Using the SI unit of magnetic flux, engineers and scientists can solve complex systems with clarity, accuracy, and repeatability.
6. Applications of Magnetic Flux in Science and Technology
Magnetic flux is not just a theoretical concept—it plays a central role in many scientific disciplines and modern technologies. The SI unit of magnetic flux, the Weber (Wb), allows engineers and researchers to quantify and optimize magnetic performance across a wide range of applications. From generating electricity to storing data, the Weber is essential for understanding and controlling electromagnetic behavior.
Below are key areas where the SI unit of magnetic flux is actively applied:
1. Electric Power Generation
In electric generators—whether powered by coal, wind, hydro, or nuclear energy—mechanical energy is converted into electrical energy by rotating coils through magnetic fields. This rotation changes the magnetic flux through the coils, inducing an electromotive force (EMF) as per Faraday’s Law:
EMF=−dtdΦ
The amount of induced voltage depends directly on the rate of change of magnetic flux measured in Webers. Accurate measurement and control of magnetic flux help optimize power output and system stability.
2. Transformers
Transformers rely on magnetic flux to transfer energy from one coil (the primary) to another (the secondary) without physical contact. The magnetic core guides the flux from one coil to the next.
Engineers design the magnetic core to handle specific values of flux, often in the range of tenths to hundreds of Webers, to ensure the transformer operates efficiently and avoids saturation.
3. Electric Motors
Electric motors use magnetic flux to create torque. Current flowing through windings generates a magnetic field, which interacts with a permanent magnet or another coil to produce rotational motion.
The SI unit of magnetic flux is used in motor design to calculate:
-
Rotor/stator magnetic interaction
-
Back-EMF (electromotive force)
-
Magnetic saturation thresholds
4. Magnetic Resonance Imaging (MRI)
MRI machines create detailed images of internal body structures using strong magnetic fields. These systems involve huge magnetic flux values, often measured in hundreds of Webers, to align the spins of hydrogen nuclei.
The SI unit of magnetic flux helps calibrate field strength and exposure levels to ensure both image accuracy and patient safety.
5. Magnetic Sensors and Hall Effect Devices
Devices like Hall effect sensors, used in automotive, robotics, and aerospace industries, measure changes in magnetic flux density. The measured signal is proportional to the amount of magnetic flux, and the Weber provides a standard unit for sensor output interpretation.
Applications include:
-
Speed and position detection
-
Brushless DC motor control
-
Current sensing in power electronics
6. Inductive Charging Systems
Wireless charging systems for smartphones and electric vehicles operate by creating time-varying magnetic flux in a primary coil, which induces current in a secondary coil. The flux transfer is optimized in units of Webers, ensuring sufficient energy delivery.
7. Data Storage: Magnetic Media
In older and some modern magnetic storage devices—like hard drives and magnetic tapes—information is stored by changing the direction of magnetic flux on a medium.
Each bit of data corresponds to a localized flux region, and the SI unit of magnetic flux is used to define flux capacity and field strength at microscopic scales.
8. Research and Material Science
Magnetic flux measurements are fundamental in the study of:
-
Superconductors: Which can exclude magnetic flux (Meissner effect)
-
Magnetic domains: In ferromagnetic materials
-
Quantum flux units: Where the smallest unit of flux is known as a fluxon
In each of these areas, the SI unit of magnetic flux supports precise experimentation and theoretical analysis.
Why Accurate Flux Measurement Matters
Incorrect calculation or estimation of magnetic flux can lead to:
-
Overheating of transformers or motors
-
Inaccurate sensor readings
-
Inefficient wireless charging
-
Safety issues in medical imaging
The use of the Weber ensures standardized, high-confidence measurement in engineering design, diagnostics, and research.
In summary, the SI unit of magnetic flux—the Weber—has practical importance in virtually every system that involves magnetism or induction. Whether designing a generator or scanning a human brain, engineers and scientists depend on the Weber to understand, quantify, and improve their technologies.
7. Common Misconceptions About Magnetic Flux and Its SI Unit
Despite its importance in physics and engineering, magnetic flux is often misunderstood—especially when it comes to its definition, its relation to other quantities, and the correct use of its unit. Clarifying these misconceptions helps students, technicians, and engineers avoid critical errors in theory and application.
Below are the most common misunderstandings related to the SI unit of magnetic flux, the Weber (Wb).
1. Confusing Magnetic Flux with Magnetic Field (Tesla)
One of the most frequent mistakes is equating magnetic flux with magnetic flux density (also known as the magnetic field).
-
Magnetic field (B) is measured in Teslas (T) and represents the intensity or strength of the field.
-
Magnetic flux (Φ) is measured in Webers (Wb) and represents the total field passing through a surface area.
Example:
A 1 T field over 2 m² gives a total magnetic flux of:
Φ=B⋅A=1⋅2=2 Wb
So, the Tesla and the Weber are not interchangeable; they describe related but distinct concepts.
2. Assuming the SI Unit of Magnetic Flux Is Rarely Used
Some assume the SI unit of magnetic flux is only used in academia or textbooks. In reality, the Weber is critical in real-world systems like:
-
Power transformers
-
Electric motors
-
Inductive sensors
-
MRI machines
-
Renewable energy generators
Without precise measurement in Webers, these technologies would fail to perform as designed.
3. Misapplying Unit Conversions Between Systems
The CGS unit of magnetic flux is the Maxwell (Mx), and some still mistakenly equate it directly with the Weber. However:
1 Wb=108 Mx
Misusing this conversion can lead to drastically wrong values in engineering calculations. The difference is exponential and must be carefully managed when switching between unit systems.
4. Believing Magnetic Flux Is Always Constant
Another misconception is that magnetic flux in a closed circuit or device remains constant. This is false—flux can change based on:
-
Angle of the magnetic field
-
Movement of a conductor
-
Varying field strength
In fact, the rate of change of magnetic flux is what induces voltage in many devices (per Faraday’s Law).
5. Thinking the Weber Is a Derived or Optional Unit
Some assume the Weber is a derived or secondary unit that can be replaced. However, the Weber is the officially recognized SI unit of magnetic flux, with a precise definition tied to the volt and second:
1 Wb=1 V⋅s
It is not optional—it is the standard, accepted globally in science and industry.
6. Overlooking the Angle in Magnetic Flux Calculations
Many students ignore the angle
θ in the flux equation:
Φ=B⋅A⋅cos(θ)
Magnetic flux is maximum when the field is perpendicular to the surface (
θ=0°,
cos(θ)=1) and zero when parallel (
θ=90°,
cos(θ)=0). Using the SI unit of magnetic flux correctly requires applying this angular dependency.
Summary of Misconceptions
| Misconception | Clarification |
|---|---|
| Flux and field are the same | No—flux (Wb) is total, field (T) is intensity |
| Weber is only academic | No—it’s widely used in engineering |
| 1 Wb = 1 Mx | False—1 Wb = 10⁸ Mx |
| Flux is always constant | False—flux varies with angle, movement, field strength |
| Weber is optional | No—it’s the official SI unit of magnetic flux |
| Angle doesn’t matter | Wrong— cos(θ) must be considered |
8. Magnetic Flux in Educational Context
Understanding magnetic flux—and correctly applying the SI unit of magnetic flux, the Weber (Wb)—is a foundational component of physics and electrical engineering education. From high school to university-level courses, magnetic flux is introduced as a gateway to more advanced electromagnetic concepts.
This section explores how the concept is taught, common learning tools, and strategies to help students grasp the meaning and use of the SI unit of magnetic flux.
How Magnetic Flux Is Taught in Schools and Universities
High School Physics Curriculum
At the introductory level, students learn:
-
Magnetic field lines and how they interact with surfaces
-
The formula
Φ=B⋅A⋅cos(θ) -
Basic applications like electromagnets and simple loops
-
Introduction to Faraday’s Law of Induction
The concept of the SI unit of magnetic flux is also introduced early on, often in relation to voltage and energy transformation in simple electrical systems.
University and Engineering Programs
In higher education, the study deepens into:
-
Electromagnetic theory
-
Vector field analysis
-
Advanced circuits and signal analysis
-
Magnetic materials and hysteresis
-
Magnetic circuit design
At this stage, precise use of the Weber as the SI unit of magnetic flux is essential for understanding how electrical machines, transformers, and magnetic sensors operate.
Lab Experiments Involving Magnetic Flux
Educational labs give students hands-on experience measuring and observing magnetic flux. Typical experiments include:
-
Magnetic flux through a coil: Students pass magnets through coils and use a voltmeter to measure induced EMF, linking the observation to Weber measurements.
-
Faraday’s coil experiment: Demonstrates how changing magnetic flux generates current, reinforcing the definition of the SI unit of magnetic flux as 1 Wb = 1 V·s.
-
Mapping magnetic field lines with iron filings and sensors: Helps visualize where and how magnetic flux is strongest.
These experiments solidify the conceptual link between theory and real-world measurements.
Visual Aids and Simulations
In modern classrooms, teachers often use:
-
Field line visualizations
-
Flux simulations (e.g., PhET simulators)
-
3D animations showing flux through loops at various angles
These tools help students understand why the SI unit of magnetic flux is important and how it relates to area, angle, and magnetic field strength.
Tips for Remembering the SI Unit of Magnetic Flux
-
Mnemonic: “Watt-Bolt” can help students associate Weber with Volt·seconds (V·s)
-
Analogy: Think of magnetic flux like “water flow through a pipe”—the Weber tells you how much magnetic “flow” goes through an area.
-
Concept Map: Connect Weber to Tesla, Volt, and Ampere for better recall.
Importance of Emphasizing Standard Units in Education
By consistently using the SI unit of magnetic flux, educators ensure students are prepared to:
-
Communicate ideas using standard language
-
Solve equations with correct dimensional analysis
-
Transition smoothly from theoretical learning to engineering practice
Emphasizing the Weber also prevents confusion when interpreting research papers, design specs, or technical standards, especially in international contexts.
9. Historical Figures Behind the Concept
The development of the concept of magnetic flux and the establishment of the SI unit of magnetic flux—the Weber (Wb)—is deeply rooted in the pioneering work of 19th-century physicists. These individuals laid the theoretical and experimental groundwork that shaped modern electromagnetism and electrical engineering.
Wilhelm Eduard Weber (1804–1891)
The Namesake of the SI Unit of Magnetic Flux
The Weber is named in honor of Wilhelm Eduard Weber, a German physicist who made foundational contributions to the study of electricity and magnetism.
Key Contributions:
-
Worked with Carl Friedrich Gauss to develop the first electromagnetic telegraph (1833), revolutionizing long-distance communication.
-
Introduced the idea of electric current as a flow of electric charge, laying the basis for modern circuit theory.
-
Conducted precise experiments on the interrelationship between electric and magnetic forces.
His work helped define the concept of electromotive force and magnetic fields, which are central to the definition of the SI unit of magnetic flux.
In 1935, the unit of magnetic flux was officially proposed to be named “Weber” in his honor, and in 1946, it was adopted into the SI system.
Michael Faraday (1791–1867)
The Father of Electromagnetic Induction
Faraday was one of the first to discover the relationship between changing magnetic fields and the generation of electric current—a phenomenon known today as Faraday’s Law.
EMF=−dtdΦ
Where
Φ is the magnetic flux measured in Webers. Although Faraday never used the SI unit of magnetic flux (as it was formalized later), his discovery directly led to the need for such a unit.
Faraday’s contributions gave rise to:
-
Transformers
-
Electric generators
-
Inductive charging
-
The principle of electromagnetic flux linkage
James Clerk Maxwell (1831–1879)
The Mathematician of Magnetism
Maxwell built upon Faraday’s work and formalized it into a comprehensive set of equations known as Maxwell’s Equations. These equations describe how electric and magnetic fields interact and propagate, and they all include terms involving magnetic flux.
His work unified:
-
Gauss’s law for electricity
-
Gauss’s law for magnetism
-
Faraday’s law of induction
-
Ampère’s circuital law (with Maxwell’s correction)
Magnetic flux, measured in the SI unit of magnetic flux, is integral to Maxwell’s equations and thus central to all of modern electromagnetism and electromagnetic wave theory.
Carl Friedrich Gauss (1777–1855)
Though more commonly associated with mathematics and statistics, Gauss also made significant contributions to magnetism, including:
-
The development of absolute magnetic measurement techniques
-
Collaborating with Weber on early electromagnetic research
His work helped shape early field theories, providing a foundation for the quantification of magnetic phenomena.
Legacy of Their Work in the SI System
The decision to define the SI unit of magnetic flux as the Weber reflects the lasting influence of these scientists. Their contributions made it possible to move from abstract phenomena to measurable, practical systems.
By naming the unit after Weber and using it in laws derived by Faraday and Maxwell, the SI system honors the collaborative legacy that built modern electromagnetic theory.
10. Summary and Key Takeaways
Magnetic flux is a core concept in electromagnetism, describing how magnetic fields interact with surfaces to induce voltage, drive current, and perform mechanical work. Understanding and measuring magnetic flux accurately is essential across disciplines like electrical engineering, physics, medical imaging, and energy generation.
The SI unit of magnetic flux, the Weber (Wb), serves as the globally recognized standard for quantifying this physical property. Its usage simplifies engineering calculations, enhances scientific communication, and ensures measurement consistency across nations, industries, and applications.
What We Covered
-
Definition of Magnetic Flux: It is the measure of magnetic field lines passing through a surface.
-
SI Unit of Magnetic Flux: The Weber (Wb), defined as 1 volt-second (V·s) or 1 Tesla·meter² (T·m²).
-
Formula:
Φ=B⋅A⋅cos(θ)where B is magnetic field strength, A is area, and θ is the angle of the field relative to the surface normal.
-
Applications:
Magnetic flux and its SI unit are foundational in transformers, generators, electric motors, MRI machines, magnetic sensors, and inductive charging systems. -
Mathematical Foundations:
The Weber connects directly to other SI units like the Tesla, Volt, Ampere, and meter. -
Historical Background:
Named after Wilhelm Eduard Weber and built on the work of Faraday, Maxwell, and Gauss, the Weber reflects a century of theoretical and experimental progress. -
Educational Relevance:
Taught in high school and university physics, magnetic flux and the Weber are introduced through simulations, experiments, and real-world analogies.
Key Takeaways
| Key Concept | Summary |
|---|---|
| Magnetic Flux | Measures the total magnetic field passing through a surface |
| SI Unit | Weber (Wb) = 1 V·s = 1 T·m² |
| Symbol | Φ (phi) |
| Applications | Generators, motors, MRI, sensors, wireless charging |
| Formula Importance | Forms the basis for Faraday’s Law of Induction |
| Historical Names | Weber (unit), Faraday (induction), Maxwell (equations) |
| Conversion | 1 Wb = 10⁸ Maxwells (CGS system) |
By mastering the concept of magnetic flux and its unit, professionals can design more efficient systems, researchers can make more accurate observations, and students can build a solid foundation in electromagnetism.
The SI unit of magnetic flux, the Weber, is more than just a unit—it is a bridge between theoretical physics and practical electrical engineering.