Pascal (Pa) is a fundamental derived unit of pressure within the International System of Units (SI), universally recognized and extensively utilized across various scientific and engineering disciplines. Defined precisely as one Newton per square meter (1 Pa = 1 N/m²), the pascal in SI units serves as the cornerstone for measuring pressure, stress, and mechanical strength, playing an indispensable role in our understanding and application of physical sciences.
Named after the influential French mathematician, physicist, and philosopher Blaise Pascal (1623–1662), the pascal was officially adopted as part of the SI system during the 14th General Conference on Weights and Measures in 1971. Pascal’s pioneering experiments and theories in fluid mechanics and hydrostatics significantly contributed to the foundational knowledge upon which modern pressure measurements and units are based.
Understanding pascal in SI units is crucial, as pressure is an omnipresent factor influencing countless phenomena—from weather patterns and climate dynamics to mechanical engineering applications, medical diagnostics, and aerospace technologies. Whether considering atmospheric pressure at sea level, fluid pressures in pipelines, or stresses within structural components, the standardized use of pascal in SI units ensures consistency, accuracy, and effective global communication among scientists, engineers, and technologists.
This article aims to provide a comprehensive understanding of what exactly pascal in SI units represents, exploring its historical background, practical significance, widespread applications, and its integral relationship within the broader SI system of measurement.
I. What Is Pascal in SI Units?
The pascal (Pa) is the SI unit of pressure, named after French mathematician and physicist Blaise Pascal. In the International System of Units (SI), it is defined as one newton of force applied uniformly over one square meter of area:
1Pa=1N/m2
This means that if a force of one newton is applied to an area of one square meter, the pressure exerted is one pascal.
SI Base Units Behind Pascal
To better understand how the pascal in SI units works, break it down into base SI units:
-
Newton (N) = kg·m/s² (force)
-
Square meter (m²) = area
So:
1Pa=1m21kg⋅m/s2=1kg⋅m−1⋅s−2
Why Use Pascal in SI Units?
The pascal provides a standardized and precise way to measure pressure in scientific and engineering contexts. Because it’s part of the SI system, it integrates smoothly with other units like newtons, meters, and seconds.
However, because 1 Pa is very small, real-world applications often use larger multiples:
-
1 kilopascal (kPa) = 1,000 Pa
-
1 megapascal (MPa) = 1,000,000 Pa
Examples of Pascal in Use
-
Atmospheric pressure at sea level: ~101,325 Pa
-
Car tire pressure: ~220 kPa
-
Concrete compressive strength: ~30 MPa
-
Human blood pressure: ~16 kPa (systolic)
II. Understanding SI Units
The International System of Units, commonly abbreviated as SI (from the French, Système International d’Unités), is the modern and globally accepted metric system for measurement. Established and maintained by the General Conference on Weights and Measures (CGPM), SI provides a coherent and standardized framework that enables accurate, consistent, and universally understood scientific and technical communication.
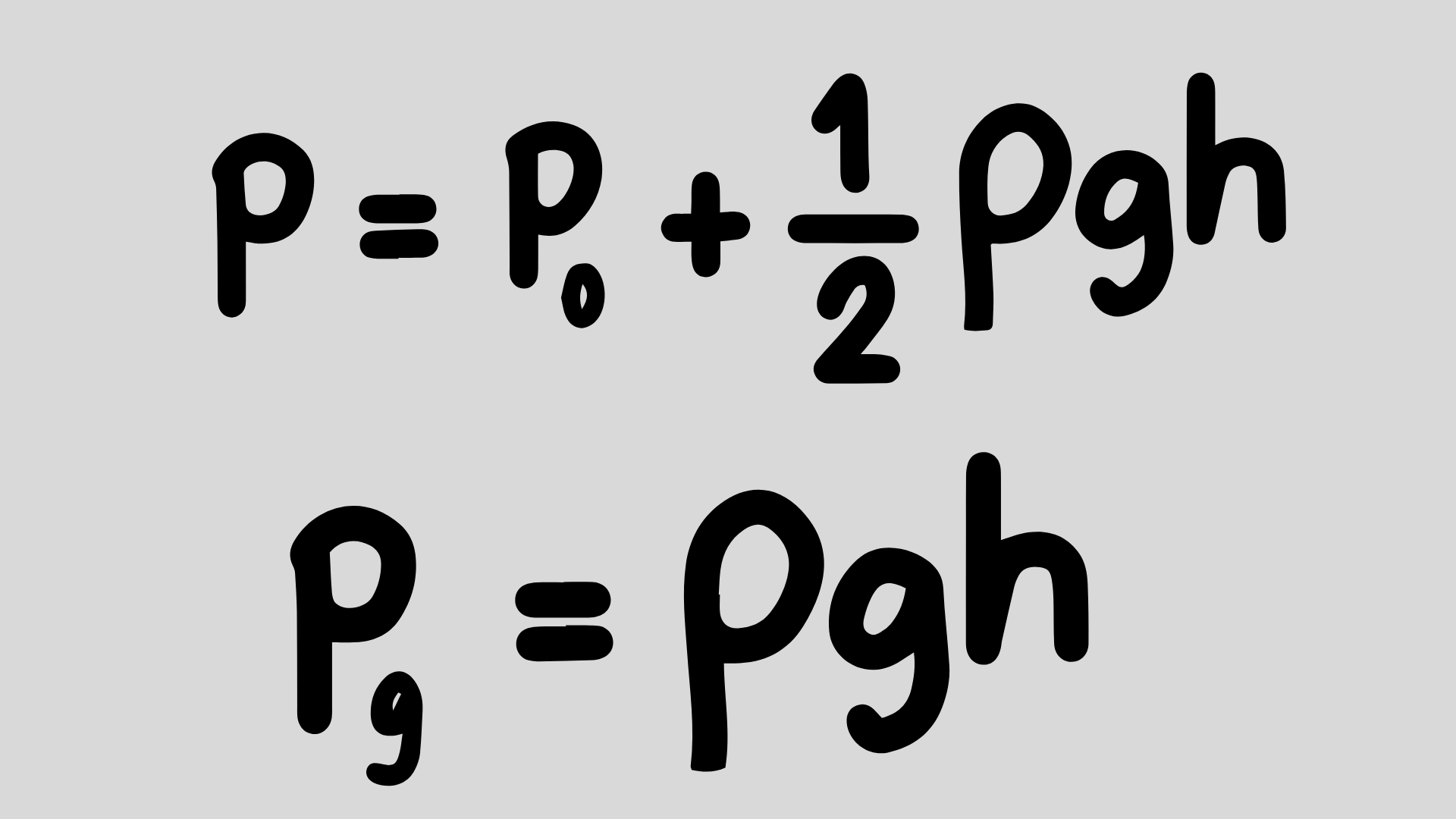
A. Origin and Purpose of SI Units
SI units originated from the metric system, which was introduced during the French Revolution in the late 18th century to standardize and simplify units of measurement. Over time, this system evolved into the International System of Units, officially established in 1960. The primary goal of the SI system is to provide clarity, uniformity, and convenience for scientists, engineers, industries, and the general public worldwide.
B. Basic Structure of SI Units
SI units are systematically categorized into two principal groups:
-
Base Units: Seven fundamental units define measurable quantities independently. These include:
-
Meter (m) – unit of length
-
Kilogram (kg) – unit of mass
-
Second (s) – unit of time
-
Ampere (A) – unit of electric current
-
Kelvin (K) – unit of temperature
-
Mole (mol) – unit of substance amount
-
Candela (cd) – unit of luminous intensity
-
-
Derived Units: These units are formed through mathematical combinations of base units to represent additional physical quantities. The Pascal (Pa) is one such derived unit, measuring pressure, defined explicitly in terms of base units (newton per square meter, N/m²).
C. Significance of Derived Units in SI
Derived units extend the functionality and practical usability of the SI system by facilitating the measurement of complex quantities encountered in real-world scenarios. Examples of widely-used derived units besides Pascal include:
-
Newton (N) – force
-
Joule (J) – energy
-
Watt (W) – power
-
Volt (V) – electric potential
The clear definition and interrelation of these derived units, including Pascal in SI units, help maintain consistency across various scientific and industrial fields.
D. Role of Pascal as a Derived Unit
Within this framework, Pascal in SI units occupies a critical role. Defined as the pressure exerted by one newton force evenly distributed over a one-square-meter surface area (1 Pa = 1 N/m²), Pascal directly links the fundamental concepts of force, mass, and area. Its clear definition and easy integration with other SI units allow professionals to reliably analyze, compute, and communicate measurements related to pressure and stress across industries and scientific disciplines.
III. Definition and Explanation of Pascal in SI Units
To understand the pascal in SI units, we must first explore what pressure is and how it is quantified within the International System of Units. Pressure is defined as the force applied per unit area. The pascal (Pa), as the SI unit of pressure, offers a standardized method to express this fundamental physical quantity.
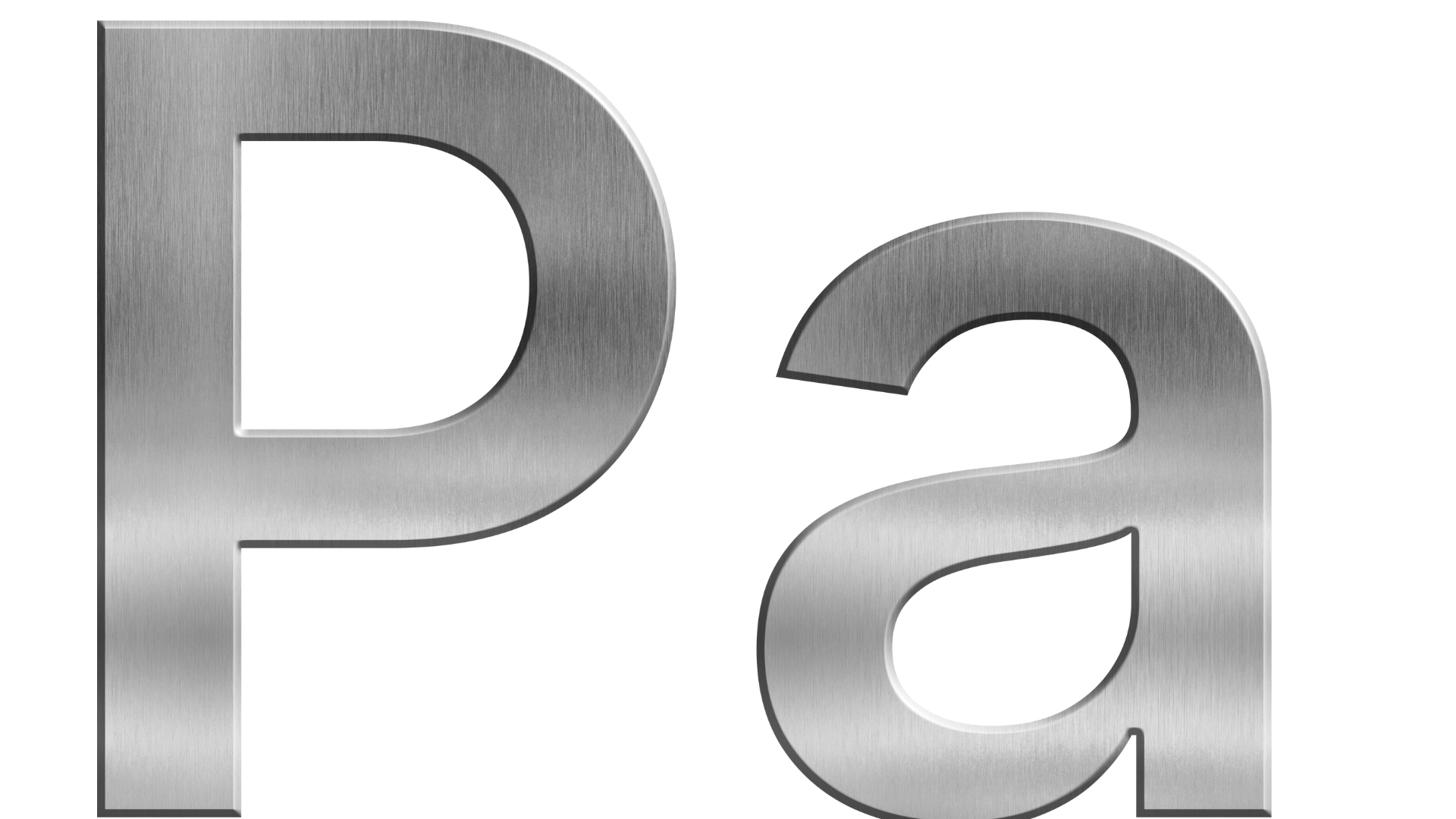
A. Formal Definition of Pascal
The pascal in SI units is formally defined as:
1 pascal (Pa) = 1 newton per square meter (1 N/m²)
This means that a pressure of one pascal is equivalent to a force of one newton acting uniformly over an area of one square meter.
Mathematically:
Pressure (Pa)=Area (m2)Force (N)
Where:
-
Newton (N) is the SI unit of force, defined as
1N=1kg⋅m/s2
-
Square meter (m²) is the SI unit of area
Thus, the pascal in SI units can be rewritten in base SI units as:
1Pa=1m21kg⋅m/s2=1kg⋅m−1⋅s−2
This formula highlights that pressure is derived from three base SI units: kilogram (mass), meter (length), and second (time).
B. Intuitive Explanation
To visualize one pascal in SI units, imagine placing a small apple (weighing approximately 100 grams or 1 newton of force) evenly on a square meter surface. The pressure exerted would be about 1 pascal — a very small pressure. Because of its small magnitude, pressure in real-world applications is often expressed in kilopascals (kPa), megapascals (MPa), or other larger units.
For example:
-
1 kPa = 1,000 Pa
-
1 MPa = 1,000,000 Pa
C. Relationship to Other Units
While the pascal in SI units is the standard for pressure measurement, other non-SI units are still in use in various industries and regions. Here’s how they compare:
-
1 atmosphere (atm) = 101,325 Pa
-
1 bar = 100,000 Pa
-
1 psi (pound per square inch) ≈ 6,894.76 Pa
-
1 torr (mmHg) ≈ 133.322 Pa
These comparisons illustrate how versatile and integrable the pascal in SI units is when converting between systems.
D. Why Use Pascal in SI Units
Using the pascal in SI units offers several advantages:
-
Standardization across global scientific and engineering communities
-
Consistency in pressure-related equations and models
-
Compatibility with all other SI base and derived units
-
Precision in calculations, particularly in simulations and computational fluid dynamics
IV. Historical Background of Pascal in SI Units
Understanding the pascal in SI units involves not only its scientific definition but also its rich historical context. The development of the unit “pascal” is deeply intertwined with the evolution of pressure science and the legacy of Blaise Pascal—a pioneering figure in fluid mechanics and physics.
A. Who Was Blaise Pascal?
Blaise Pascal (1623–1662) was a French mathematician, physicist, inventor, writer, and philosopher. Despite his short life, he made groundbreaking contributions to various fields, particularly in the realm of fluid dynamics and pressure.
His most notable achievements related to pressure include:
-
Pascal’s Principle: Demonstrated that a pressure change at any point in a confined fluid is transmitted undiminished throughout the fluid.
-
Barometric Experiments: Proved that atmospheric pressure decreases with altitude, using mercury-filled tubes and mountain measurements.
These studies laid the groundwork for the modern understanding of pressure and formed the basis for naming the SI pressure unit after him.
B. The Evolution of Pressure Measurement
Before the pascal in SI units was formally introduced, pressure was measured using various local and traditional systems such as:
-
Millimeters of mercury (mmHg)
-
Atmospheres (atm)
-
Pounds per square inch (psi)
These units were often inconsistent and difficult to convert, especially across different disciplines and international borders.
C. Adoption of Pascal into the SI System
The move toward international standardization began in earnest with the establishment of the International System of Units (SI) in 1960. As part of this global shift, the need for a standardized pressure unit became clear.
In 1971, during the 14th General Conference on Weights and Measures (CGPM), the pascal was officially adopted as the SI unit of pressure. The decision to name the unit “pascal” honored Blaise Pascal’s significant scientific contributions.
From then on, the pascal in SI units became the reference standard for pressure, stress, and similar quantities across science, engineering, meteorology, and industry.
D. Early Uses and Promotion
Once adopted, organizations such as:
-
The International Bureau of Weights and Measures (BIPM)
-
The International Organization for Standardization (ISO)
-
National standards bodies and scientific institutions
began promoting the use of pascal in SI units. Gradually, textbooks, research papers, and technical documentation transitioned away from older pressure units in favor of pascal and its derivatives (kPa, MPa, etc.).
E. Impact of Standardization
The historical adoption of the pascal in SI units marked a major milestone in measurement standardization. It:
-
Eliminated confusion across different pressure systems
-
Improved accuracy and clarity in scientific communication
-
Supported international collaboration in engineering, science, and manufacturing
V. Importance and Application of Pascal in SI Units
The pascal in SI units is not just a theoretical concept—it plays a vital role in practical applications across many scientific and engineering disciplines. Its use enables accurate, standardized pressure measurement that is essential for safety, performance, and innovation in both everyday and highly specialized settings.
A. Why the Pascal in SI Units Is Important
The importance of using pascal in SI units lies in several key factors:
-
Standardization Across Industries
Using a consistent pressure unit allows engineers, scientists, and manufacturers worldwide to collaborate, exchange data, and follow universal protocols without confusion or conversion errors. -
Precision and Accuracy
The pascal provides a well-defined and exact unit for calculating pressure-related phenomena, which is crucial in safety-critical fields like aerospace and medicine. -
Integration with Other SI Units
Because the pascal is derived from the SI base units (kilogram, meter, second), it seamlessly fits into equations involving force, area, stress, and energy.
B. Scientific Applications of Pascal in SI Units
-
Fluid Mechanics
In studying fluid flow and pressure drop through pipes and channels, the pascal is fundamental for calculations involving hydraulic pressure, head loss, and pump selection. -
Atmospheric Science
Meteorologists use pascals to describe atmospheric pressure. Standard atmospheric pressure at sea level is 101,325 Pa, a benchmark used in weather forecasting and climate models. -
Material Science and Physics
Stress and strain analysis depend on pressure measurements in pascals. Engineers use MPa (megapascals) to assess a material’s yield strength and failure limits. -
Thermodynamics
In thermodynamic systems, pascal is used to quantify internal and external pressure, influencing phase changes, boiling points, and gas behaviors under different conditions.
C. Engineering Applications of Pascal in SI Units
-
Mechanical Engineering
Pascal is used to design and evaluate components like pressure vessels, hydraulic actuators, and compressors, ensuring they can withstand expected pressures. -
Civil Engineering
Structural loading and stress distribution are calculated in pascals, especially for bridges, dams, and high-rise buildings, where safety margins depend on accurate pressure readings. -
Aerospace Engineering
Aircraft design depends on pascals to model air pressure, cabin pressurization, and aerodynamic forces that affect flight performance. -
Automotive Engineering
Engine combustion pressure, tire pressure, and brake hydraulics are all measured in kilopascals (kPa) or megapascals (MPa), enhancing performance and safety.
D. Industrial and Everyday Uses
-
Medical Devices
Blood pressure is often measured in mmHg, but modern equipment translates it internally to pascals for precise readings. Ventilators and IV systems also rely on pressure control using pascals. -
Manufacturing and Quality Control
Pneumatic and hydraulic systems in factories operate under precise pressure conditions expressed in pascal-based units. -
HVAC Systems
Heating, ventilation, and air conditioning systems use pascal readings to control air pressure in ducts, filters, and ventilation zones. -
Tire Inflation and Safety Checks
Tire pressures are commonly displayed in kilopascals (kPa), which reflect the internal air pressure needed for optimal vehicle performance and safety.
E. Derivatives and Practical Ranges
Because 1 pascal is relatively small, it’s common to use:
-
kPa (kilopascal) for weather, car tires, and HVAC (e.g., 100 kPa = 1 bar)
-
MPa (megapascal) for material strength and hydraulics (e.g., steel yield strength ≈ 250 MPa)
-
GPa (gigapascal) for extreme pressures like those inside the Earth or during high-pressure physics experiments
VI. Conversion of Pascal in SI Units to Other Pressure Units
While the pascal in SI units is the globally standardized unit for pressure, various fields and regions still use alternative pressure units such as bar, psi (pounds per square inch), atmosphere (atm), and torr. For clarity, accuracy, and cross-system communication, it’s essential to understand how to convert the pascal in SI units to these other commonly used pressure measurements.
A. Why Convert Pascal in SI Units?
Although the SI system promotes universal usage, many industries or regions retain older systems due to historical preferences or practical reasons. Examples include:
-
psi in the United States for tire pressure and hydraulics
-
bar in Europe for industrial applications
-
mmHg or torr in medical and laboratory settings
-
atmospheres in chemistry and meteorology
Understanding how to convert pascal in SI units ensures compatibility and consistency across international standards and technical documentation.
B. Common Conversion Factors
Here are the most widely used conversions from pascal in SI units to other pressure units:
| Pressure Unit | Equivalent in Pascal (Pa) |
|---|---|
| 1 bar | 100,000 Pa |
| 1 atmosphere (atm) | 101,325 Pa |
| 1 psi | 6,894.76 Pa |
| 1 torr (mmHg) | 133.322 Pa |
| 1 mm H₂O | 9.80665 Pa |
| 1 kPa | 1,000 Pa |
| 1 MPa | 1,000,000 Pa |
C. Example Conversion Calculations
1. Convert 200,000 Pa to bar:
200,000Pa÷100,000=2bar
2. Convert 1 atm to Pa:
1atm=101,325Pa
3. Convert 500,000 Pa to psi:
500,000Pa÷6,894.76≈72.52psi
4. Convert 101,325 Pa to mmHg:
101,325Pa÷133.322≈760mmHg
D. Tools for Conversion
To streamline these calculations, many professionals use:
-
Digital pressure gauges with multiple unit options
-
Online pressure unit converters
-
Engineering calculator apps
-
Spreadsheet functions in Excel or Google Sheets
For example:
=CONVERT(101325, "Pa", "psi") → Returns approx. 14.7 psi
E. Importance of Precision
In sensitive applications such as:
-
Medical equipment
-
High-pressure industrial systems
-
Laboratory calibration
Even minor conversion errors from pascal in SI units can lead to system malfunctions, safety risks, or invalid results. Always ensure the correct number of significant figures and unit consistency.
F. Common Mistakes to Avoid
-
Mixing up bar and atm – Though close, 1 bar ≠ 1 atm (bar is slightly less)
-
Using outdated units – mmHg or inches of mercury (inHg) are being phased out in many scientific fields
-
Ignoring unit prefixes – Confusing kPa and Pa can result in 1000× errors
G. Summary Table: Quick Reference
| From → To | Multiply by |
|---|---|
| Pa → bar | 0.00001 |
| Pa → atm | 9.8692 × 10⁻⁶ |
| Pa → psi | 0.000145038 |
| Pa → torr | 0.00750062 |
| Pa → mm H₂O | 0.10197 |
**VII. How to Measure Pascal in SI Units
Measuring pascal in SI units involves quantifying the amount of force applied over a specific area. In real-world applications, this is done using a variety of mechanical and electronic instruments designed to detect and display pressure values accurately. From scientific laboratories to industrial plants and medical devices, the ability to measure pressure in pascals is essential for system monitoring, safety, and performance.
A. The Principle Behind Measuring Pascal in SI Units
Since 1 pascal = 1 newton per square meter (N/m²), measuring pascal in SI units essentially means determining how much force is being applied to a known area.
The general formula used:
Pressure (Pa)=Area (m²)Force (N)
Most pressure-measuring instruments are designed to either directly or indirectly calculate this ratio and display the pressure in pascals or a related unit (kPa, MPa).
B. Common Instruments for Measuring Pascal in SI Units
-
Manometers
-
U-tube manometers use a column of liquid (usually water or mercury) to compare pressure.
-
The difference in liquid levels translates to pressure, which can be converted into pascals.
-
Suitable for simple, low-pressure measurements.
-
-
Bourdon Tube Gauges
-
Widely used in mechanical pressure measurement.
-
Pressure causes a curved metal tube to straighten; this movement is linked to a dial calibrated in kPa or psi, which can be converted to pascal in SI units.
-
-
Digital Pressure Sensors
-
Use piezoelectric or capacitive elements that deform under pressure.
-
Output is converted electronically to digital readouts in pascal-based units.
-
Extremely accurate and widely used in automation, medical, and aerospace applications.
-
-
Strain Gauge Transducers
-
Measure deformation (strain) in a diaphragm caused by pressure.
-
The electrical resistance change is measured and converted to pressure in pascals.
-
Suitable for high-pressure, high-precision applications.
-
-
Barometers (for atmospheric pressure)
-
Measure ambient atmospheric pressure, typically in hPa (hectopascals).
-
Common in meteorology and aviation.
-
C. Measurement Ranges and Unit Scaling
Because the pascal in SI units is a relatively small unit, most instruments display pressure in scaled forms:
-
Pa – Used in ultra-low-pressure applications (e.g., clean rooms, HVAC differential pressure).
-
kPa (kilopascal) – Common in weather reports and car tires.
-
MPa (megapascal) – Used in structural engineering, hydraulic systems, and high-pressure machinery.
Example: A tire pressure of 32 psi ≈ 220 kPa or 220,000 Pa
D. Calibration and Accuracy
To ensure accurate readings in pascal in SI units, all instruments must be:
-
Calibrated regularly using standard weights or pressure sources
-
Maintained to avoid sensor drift or physical damage
-
Compensated for temperature and other environmental factors
Certified calibration against national or international standards (e.g., NIST, ISO) ensures the traceability of measurements.
E. Applications in Real-World Scenarios
-
Medical Devices: Blood pressure monitors and ventilators measure low-range pressures in mmHg but internally use pascals for calculation.
-
Industrial Automation: Process control systems use pressure sensors with 4–20 mA signals converted to kPa or MPa.
-
Research and Testing: Laboratory experiments often measure air or fluid pressure in precise pascal units to study flow dynamics or material behavior.
F. Measurement Best Practices
-
Select the right sensor for your pressure range
-
Avoid overpressure to prevent sensor damage or inaccurate readings
-
Use compatible units when integrating sensors into control systems
-
Record readings digitally for traceability and further analysis
G. Software and Data Logging
Modern pressure measurement systems often integrate:
-
Data acquisition software
-
Wireless sensors with Bluetooth or IoT
-
Cloud-based dashboards displaying pressure in pascal in SI units in real time
These technologies allow pressure to be continuously monitored, archived, and analyzed for performance optimization.
VIII. Pascal in SI Units and Its Significance in Science
The pascal in SI units is more than just a pressure measurement—it is a fundamental building block in the scientific understanding of force, energy, and matter interactions. In both theoretical and experimental science, the pascal enables researchers to quantify and model pressure-related phenomena across physics, chemistry, biology, environmental studies, and engineering.
A. Foundation for Physical Sciences
-
Fluid Dynamics and Hydrodynamics
In the study of how fluids (liquids and gases) move and interact with surfaces, pascal in SI units is used to measure pressure gradients. These gradients drive fluid motion and influence behaviors such as turbulence, laminar flow, and cavitation. -
Gas Laws in Thermodynamics
Scientific principles like Boyle’s Law, Charles’s Law, and the Ideal Gas Law use pressure as a key variable. The use of pascal in SI units ensures consistency in calculating relationships between pressure, volume, and temperature in gas systems:PV=nRT
Where pressure (P) is always expressed in pascals in SI-based calculations.
-
Solid Mechanics and Stress Analysis
In materials science, pressure in pascals is used to define:-
Stress (σ) = force/area (Pa)
-
Elastic modulus (Young’s modulus) = stress/strain (Pa)
-
Yield strength and fracture limits (measured in MPa or GPa)
-
B. Atmospheric Science and Meteorology
-
Air Pressure and Weather Forecasting
Atmospheric pressure is a crucial parameter in meteorology. It influences wind, precipitation, and storm systems. The hectopascal (hPa) is commonly used in weather maps (1 hPa = 100 Pa). -
Altitude and Pressure
Atmospheric pressure decreases with altitude. Scientists use pascal-based measurements to determine:-
Altitude in aviation
-
Oxygen availability
-
Barometric trends in climate studies
-
-
Climate Modeling
Complex climate models rely on consistent pressure data in pascal in SI units to simulate interactions between the atmosphere, oceans, and biosphere.
C. Biology and Medicine
-
Cellular and Molecular Pressure
Scientists studying biological membranes, osmosis, and turgor pressure use pascal-based units to quantify pressure differences across cellular structures. -
Respiratory and Cardiovascular Research
Blood pressure, pulmonary pressure, and intracranial pressure are commonly measured in mmHg but can be converted into pascal for standardized research and simulation.
D. Space and Planetary Sciences
-
Vacuum and Low-Pressure Environments
In space science, pressures often fall below 1 Pa. Instruments such as vacuum gauges measure ultra-low pressures in micro- and nano-pascals to study:-
Outer space conditions
-
Satellite chamber environments
-
Spacecraft propulsion systems
-
-
Planetary Atmospheres
Scientists use pascal in SI units to express atmospheric pressures on other planets:-
Mars: ~610 Pa
-
Venus: ~9.2 MPa
-
E. Chemistry and Reaction Dynamics
-
Partial Pressure of Gases
In chemical reactions involving gases, partial pressure is critical. Using pascal in SI units allows precise control in:-
Combustion
-
Gas-phase synthesis
-
Catalyst testing
-
-
Pressure in Equilibrium Systems
Le Chatelier’s principle and reaction kinetics depend on pressure changes. Experiments often require pressure control and recording in pascals.
F. Acoustic Science and Sound Pressure
-
Sound Pressure Level (SPL)
The intensity of sound is measured using pascal in SI units. The reference sound pressure in air is:20μPa (20 millionths of a pascal)
This extremely small unit shows the flexibility and range of the pascal in acoustic measurements.
-
Ultrasound and Sonar Applications
Research in medical imaging, underwater navigation, and non-destructive testing uses precise pressure measurements in pascals to characterize acoustic waves.
G. Significance in Research and Innovation
The standardized use of pascal in SI units allows:
-
International research collaboration
-
Replication of scientific experiments
-
Accurate data modeling in simulations
-
Development of new technologies that depend on pressure-controlled environments (e.g., microfluidics, semiconductors, nanotechnology)
H. Summary of Scientific Relevance
| Field | Role of Pascal in SI Units |
|---|---|
| Physics | Pressure, stress, fluid behavior |
| Meteorology | Atmospheric pressure and climate modeling |
| Medicine | Blood and respiratory pressure measurements |
| Chemistry | Gas laws, partial pressure, equilibrium shifts |
| Space Science | Vacuum systems, planetary atmospheres |
| Acoustics | Sound pressure level and ultrasound calibration |
IX. Pascal in SI Units in Engineering
The pascal in SI units is one of the most important units used in engineering disciplines. As the standard unit of pressure, stress, and load intensity, the pascal underpins engineering calculations, system designs, structural analysis, and safety protocols across mechanical, civil, aerospace, automotive, and process engineering fields.
A. Mechanical Engineering Applications
-
Hydraulic and Pneumatic Systems
Pressure is a core operating parameter in hydraulic presses, cylinders, and pneumatic actuators. Engineers use kilopascals (kPa) or megapascals (MPa) to design systems that can safely and efficiently transmit force via fluid power. -
Machine Design and Component Stress
Engineers use pascal in SI units to calculate internal stresses in machine components. For example:-
Stress (σ) = Force / Area → measured in Pa
-
Allowable stress is compared to material yield strength (MPa or GPa)
-
-
Boilers and Pressure Vessels
The design of pressure vessels must comply with codes like ASME, which specify maximum allowable working pressure (MAWP) in pascals or MPa. Precise pressure calculations help prevent catastrophic failures.
B. Civil and Structural Engineering
-
Structural Load Analysis
In structures such as bridges, buildings, and dams, pascal in SI units is used to express pressure from wind, water, or soil. These pressures affect structural stability and material selection. -
Geotechnical Engineering
Soil bearing pressure and earth pressure against retaining walls are measured in kPa, ensuring safe foundation and slope designs. -
Concrete and Reinforced Structures
The compressive strength of concrete is typically expressed in MPa. For example:-
Standard concrete may have a compressive strength of 20–40 MPa
-
High-performance concrete can exceed 100 MPa
-
C. Aerospace Engineering
-
Aerodynamic Pressure
Engineers use pascal in SI units to analyze pressure distribution over aircraft surfaces. This is essential for lift, drag, and stability calculations. -
Cabin Pressurization Systems
Aircraft cabins are pressurized to maintain safe and comfortable conditions for passengers, often measured in kPa relative to outside pressure. -
Rocket Propulsion and High-Altitude Conditions
Thrust chamber pressure, vacuum environments, and altitude simulations rely on extremely accurate pressure readings in pascal in SI units, sometimes down to micro-pascals.
D. Automotive Engineering
-
Tire Pressure
Tire inflation is usually specified in kilopascals (kPa). Maintaining correct tire pressure improves fuel efficiency, performance, and safety. -
Engine Combustion Analysis
Cylinder pressure is measured in MPa to analyze combustion efficiency, power output, and engine diagnostics. -
Brake Systems and Hydraulics
Hydraulic braking systems operate under pressure, often expressed in pascal in SI units, to ensure force transmission from the pedal to the brake pads.
E. Process and Chemical Engineering
-
Pipeline Pressure Monitoring
Engineers monitor pressure inside gas and liquid pipelines in pascal in SI units to maintain safe flow rates and prevent rupture. -
Pressure in Reactors and Storage Tanks
Chemical processes often involve reactions under pressure. The pascal is used to define operating limits and control conditions in reactors and tanks. -
Instrumentation and Control
Process automation systems rely on sensors and transmitters that output pressure readings in kPa or MPa for process control loops.
F. Electrical and Electronics Engineering
-
Sensor Design
MEMS (Micro-Electro-Mechanical Systems) pressure sensors are calibrated in pascal to measure environmental and internal pressures in devices. -
Vacuum Technology
Engineers working with vacuum chambers for semiconductor fabrication or electronic testing use micro-pascals (μPa) to describe low-pressure conditions.
G. Standard Engineering Units Derived from Pascal
Engineers often use larger or smaller units derived from the pascal in SI units to match practical measurement scales:
| Unit | Value in Pa | Common Use Example |
|---|---|---|
| kPa | 1,000 Pa | Tire pressure, water systems |
| MPa | 1,000,000 Pa | Steel strength, hydraulics |
| GPa | 1,000,000,000 Pa | Material stiffness (e.g., Young’s Modulus) |
| hPa | 100 Pa | Atmospheric science |
H. Engineering Design Codes and Standards
Many engineering standards explicitly use pascal in SI units:
-
ASME Boiler & Pressure Vessel Code
-
Eurocode for structural design
-
ISO 5167 for flow measurement
-
NFPA standards for fire sprinkler pressure requirements
These documents ensure consistent use of pressure data in design, safety margins, and legal compliance.
I. Summary of Engineering Applications
| Discipline | Use of Pascal in SI Units |
|---|---|
| Mechanical Engineering | Hydraulic force, component stress |
| Civil Engineering | Load analysis, soil pressure |
| Aerospace Engineering | Aerodynamics, cabin pressure |
| Automotive Engineering | Tire and brake pressure, combustion analysis |
| Process Engineering | Pipeline and reactor design |
| Electronics | Vacuum and sensor calibration |
X. Advantages and Limitations of Using Pascal in SI Units
The pascal in SI units is a powerful and essential tool for measuring pressure in modern science and engineering. As with any standardized unit, it offers numerous advantages but also comes with certain limitations depending on the context in which it is used. Understanding both its strengths and weaknesses is crucial for effective application.
A. Advantages of Using Pascal in SI Units
1. Global Standardization
The pascal in SI units is recognized and used worldwide, making it the universal language of pressure measurement. This global standardization:
-
Facilitates international collaboration in research and engineering
-
Ensures compatibility in documentation, instrumentation, and communication
-
Reduces errors caused by unit conversions
2. Coherent with Other SI Units
The pascal is a derived SI unit, defined as 1 N/m². It integrates seamlessly with other SI units such as:
-
Newton (N) for force
-
Meter (m) for area
-
Kilogram (kg), second (s) for fundamental calculations
This coherence supports accurate equations and models in physics, thermodynamics, and structural analysis.
3. Scalable Across Magnitudes
The pascal in SI units can be scaled easily to suit applications of different sizes:
-
kPa (kilopascal) for tire pressure, weather
-
MPa (megapascal) for structural and hydraulic engineering
-
GPa (gigapascal) for high-pressure materials science
-
μPa (micropascal) for sensitive acoustic or vacuum measurements
4. Easy Integration with Digital Systems
Modern sensors and data systems often operate using SI units. Using pascal:
-
Simplifies digital readouts and instrumentation
-
Enhances compatibility with control systems, IoT, and SCADA platforms
-
Improves data logging and reporting accuracy
5. Versatile Across Industries
The pascal is used in a vast range of industries and applications, such as:
-
Meteorology
-
Aerospace
-
Automotive
-
Chemical processing
-
Civil engineering
-
Medical technology
B. Limitations of Using Pascal in SI Units
1. Low Base Unit Magnitude
One pascal (1 Pa) represents a very small amount of pressure:
1Pa=1N/m2
This makes it impractical for many everyday or industrial scenarios. For example:
-
Standard atmospheric pressure is 101,325 Pa
-
Steel yield strength may be 250,000,000 Pa (250 MPa)
This often requires users to work in kPa, MPa, or other larger units, increasing complexity.
2. Lack of Familiarity in Some Regions
In countries like the United States, non-SI units such as psi (pounds per square inch) remain prevalent. This can lead to:
-
Communication gaps between international teams
-
Confusion or errors in pressure values
-
Need for constant unit conversions
3. Confusion Between Similar Units
Users may sometimes confuse:
-
Pascal (Pa) and bar (1 bar = 100,000 Pa)
-
kPa and Pa (1 kPa = 1,000 Pa)
-
atm and Pa (1 atm = 101,325 Pa)
Mistakes in scaling can result in significant design or operational errors.
4. Instrument Calibration Requirements
Accurate measurement in pascal units requires properly calibrated instruments. Inaccurate sensors or poor maintenance can lead to:
-
Drift in readings
-
Faulty calculations
-
Safety issues in critical systems
C. Comparison Summary
| Feature | Advantage | Limitation |
|---|---|---|
| Global Recognition | Universally accepted and understood | Less used in certain countries (e.g., U.S.) |
| Unit Size | Scalable for diverse applications | Base unit is very small and often requires prefixes |
| SI System Integration | Seamless with physics and engineering equations | Can cause confusion if SI literacy is low |
| Digital Compatibility | Ideal for modern sensors and automation | Requires regular calibration for accuracy |
| Communication | Enhances scientific and technical consistency | Conversion may be needed for legacy systems |
D. Best Practices for Overcoming Limitations
To maximize the benefits of the pascal in SI units:
-
Use appropriate prefixes (kPa, MPa, etc.) for clarity and practicality
-
Train personnel on SI unit conversions and usage
-
Implement standardized documentation using SI pressure units
-
Regularly calibrate pressure instruments to maintain data integrity
-
Use conversion tools for cross-unit communication in international projects
XI. Examples and Practical Uses of Pascal in SI Units
The pascal in SI units is not just a scientific abstraction—it plays a crucial role in many real-world applications. From monitoring atmospheric conditions to designing complex engineering systems, pascal-based measurements help us understand and control the forces acting on materials, fluids, and gases. This section explores practical, relatable examples of how pascal in SI units is used in daily life, industrial settings, and technical disciplines.
A. Atmospheric Pressure
One of the most common uses of the pascal in SI units is to measure atmospheric pressure.
-
Standard atmospheric pressure at sea level is defined as:
101,325Pa=1atm
-
Meteorologists often use hectopascals (hPa) or kilopascals (kPa):
-
1013.25 hPa or 101.325 kPa = 1 atm
-
Use case: Weather forecasts often mention atmospheric pressure in hPa to predict changes in weather patterns, like storms or high-pressure systems.
B. Tire Pressure
Car tires are typically inflated to pressures in the kilopascal range.
-
Example:
-
A passenger car tire may require 220 kPa.
-
That’s equivalent to 32 psi or 220,000 pascals.
-
Use case: Maintaining proper tire pressure ensures fuel efficiency, tire longevity, and safety.
C. Hydraulic Systems
Hydraulic presses and brake systems operate under high pressure, commonly measured in megapascals (MPa).
-
Example:
-
A hydraulic system in a factory press may run at 10 MPa (10 million pascals).
-
Use case: Pascal in SI units helps determine whether the hydraulic components can withstand operational loads without failure.
D. Structural Engineering
The strength of construction materials, such as concrete and steel, is specified in megapascals.
-
Concrete compressive strength:
-
Ordinary concrete: ~20–40 MPa
-
High-performance concrete: 60+ MPa
-
-
Structural steel yield strength:
-
Common grades: 250–550 MPa
-
Use case: Engineers use pascal-based units to ensure buildings, bridges, and dams can support expected loads.
E. Medical Applications
Blood pressure is traditionally measured in mmHg, but internally, modern equipment often uses pascals.
-
Normal human blood pressure:
-
120/80 mmHg ≈ 16,000/10,700 Pa
-
Use case: Ventilators and IV pumps use digital pressure sensors calibrated in pascals for accurate, automated operation.
F. Vacuum and Space Technology
Vacuum systems, especially in scientific research and space applications, use very low pressures expressed in micropascals (μPa) or even nanopascals (nPa).
-
Space vacuum pressure: less than 1 μPa
-
Laboratory vacuum chambers: 10⁻⁵ to 10⁻⁸ Pa
Use case: Accurate pressure control is critical in semiconductor manufacturing, space simulations, and high-energy physics experiments.
G. Fluid Flow and Pumping Systems
Engineers use pascal in SI units to calculate pressure drops in pipelines and size pumps accordingly.
-
Example:
-
A water distribution pipeline may operate at 300–500 kPa.
-
Engineers use pascals to assess flow efficiency and energy loss.
-
Use case: Designing municipal water supply networks or industrial coolant systems.
H. HVAC (Heating, Ventilation, and Air Conditioning)
Pascal-based pressure measurements are essential for balancing airflows and maintaining ventilation efficiency.
-
Static pressure in ducts: typically around 250–500 Pa
-
Differential pressure across filters: 50–250 Pa
Use case: Ensuring adequate airflow and air quality in commercial buildings and cleanrooms.
I. Acoustics and Sound Measurement
Sound pressure levels (SPL) are referenced to 20 μPa, which is the threshold of human hearing.
-
A loud concert may reach:
SPL=100dB=2Pa
Use case: Engineers use pascals to design audio systems and ensure occupational noise limits.
J. Aviation and Aerospace Engineering
Cabin pressurization and aerodynamic performance rely heavily on pressure measurements.
-
Cabin pressure is maintained at ~75–80 kPa
-
External pressure at cruising altitude drops to ~22 kPa
Use case: Accurate measurement of pascal in SI units ensures passenger safety and optimal aircraft performance.
K. Laboratory and Research Equipment
Scientific instruments often require controlled pressure environments:
-
Autoclaves for sterilization: 0.2–0.3 MPa
-
Gas cylinders in chemistry labs: up to 15 MPa
Use case: Researchers rely on pressure data in pascals to carry out controlled, replicable experiments.
Summary Table: Common Applications of Pascal in SI Units
| Application Area | Typical Pressure Range | Unit Equivalent |
|---|---|---|
| Atmospheric Pressure | 101,325 Pa | 1 atm |
| Car Tire Inflation | 200–250 kPa | 29–36 psi |
| Hydraulic Systems | 5–30 MPa | 725–4,351 psi |
| Concrete Strength | 20–60 MPa | High-performance |
| Blood Pressure | 10–17 kPa | 80–120 mmHg |
| Vacuum Chambers | <1 Pa | Scientific research |
| Sound Pressure (SPL) | 20 μPa – 2 Pa | Threshold to loud |
| HVAC Systems | 50–500 Pa | Low-pressure airflow |
XII. Common Misconceptions and Clarifications About Pascal in SI Units
While the pascal in SI units is a standardized and widely accepted measure of pressure, misunderstandings can arise—especially among students, new engineers, or those transitioning from imperial or non-SI systems. This section addresses common misconceptions and provides clear explanations to prevent confusion and ensure proper usage.
A. Misconception 1: Pascal Is a Large Unit of Pressure
Reality:
The pascal in SI units is actually quite small. One pascal is the pressure of one newton of force applied over one square meter of area.
1Pa=1N/m2
To give perspective:
-
Standard atmospheric pressure = 101,325 Pa
-
Common tire pressure = 220,000 Pa (220 kPa)
Clarification:
Due to its small size, pressure is often expressed in kilopascals (kPa), megapascals (MPa), or even gigapascals (GPa), depending on the application.
B. Misconception 2: Pascal and PSI Are Interchangeable Without Conversion
Reality:
PSI (pounds per square inch) is a non-SI unit primarily used in the United States. It is not numerically equivalent to pascal.
1psi≈6,894.76Pa
Clarification:
Always use correct conversion factors. For example:
-
100,000 Pa = 14.5 psi
-
250 psi ≈ 1.72 MPa
Failing to convert properly can result in serious engineering errors.
C. Misconception 3: Pascal and Bar Are the Same
Reality:
Although similar, 1 bar is defined as 100,000 pascals, which is slightly less than 1 atmosphere (101,325 Pa).
Clarification:
Use pascal in SI units for scientific accuracy and standardization. The bar is not an SI unit, though it’s still used in some industries (e.g., scuba diving, meteorology).
D. Misconception 4: kPa and Pa Can Be Used Interchangeably
Reality:
1 kilopascal (kPa) = 1,000 pascals (Pa).
Clarification:
Misunderstanding or mislabeling units can result in errors by a factor of 1,000. Always double-check whether values are in Pa, kPa, or MPa, especially when programming sensors or interpreting datasheets.
E. Misconception 5: Pascal Measures Force
Reality:
Pascal measures pressure, which is force per unit area—not force alone.
Clarification:
-
Force is measured in newtons (N)
-
Pressure is measured in pascals (Pa)
-
Relationship:
Pa=N/m2
For example, the same force over a smaller area produces higher pressure.
F. Misconception 6: Atmospheric Pressure Is Always 100,000 Pa
Reality:
Standard atmospheric pressure is more precisely defined as 101,325 Pa, not exactly 100,000 Pa.
Clarification:
The value 100,000 Pa (1 bar) is often used for convenience, but it’s important to know the precise figure when working in fields like meteorology, aviation, and fluid dynamics.
G. Misconception 7: mmHg and Pa Are Completely Separate Concepts
Reality:
mmHg (millimeters of mercury) is a unit of pressure based on the height of a mercury column. It is commonly used in medical and laboratory settings.
1mmHg≈133.322Pa
Clarification:
mmHg and Pa measure the same physical quantity—pressure. Many digital instruments now convert mmHg into pascal internally for standardization.
H. Misconception 8: Pascal Is Only Used in Science, Not in Everyday Life
Reality:
The pascal in SI units is widely used in engineering, automotive, medical, meteorological, and industrial contexts.
Clarification:
Even if not visible to the end-user, devices like tire pressure gauges, weather stations, and blood pressure monitors often use pascal-based readings internally.
I. Misconception 9: Only Absolute Pressure Is Expressed in Pascals
Reality:
Pascals can represent:
-
Absolute pressure (measured from a perfect vacuum)
-
Gauge pressure (measured relative to atmospheric pressure)
-
Differential pressure (difference between two pressures)
Clarification:
Always clarify which type of pressure is being referred to (Pa absolute, Pa gauge, etc.) to avoid misinterpretation.
J. Summary Table: Misconceptions and Clarifications
| Misconception | Clarification |
|---|---|
| Pascal is a large unit | 1 Pa is very small; use kPa or MPa in practice |
| Pa and psi are interchangeable | Conversion is needed (1 psi ≈ 6,894.76 Pa) |
| Pascal = bar | 1 bar = 100,000 Pa, but bar is not an SI unit |
| Pa = kPa | 1 kPa = 1,000 Pa; confusing them causes big errors |
| Pascal measures force | Pa = force per unit area (N/m²), not force alone |
| Atmospheric pressure = 100,000 Pa | Exact value is 101,325 Pa |
| mmHg is not related to Pa | 1 mmHg ≈ 133.322 Pa |
| Pascal is only for scientists | Used in tires, medicine, engineering, weather, etc. |
| Pascal only measures absolute pressure | Also used for gauge and differential pressure |
XIII. Frequently Asked Questions (FAQs) About Pascal in SI Units
To reinforce understanding and address common queries, here are answers to frequently asked questions about the pascal in SI units. These cover basic definitions, conversions, and practical applications relevant to students, engineers, and general users.
1. What exactly does one pascal represent?
Answer:
One pascal (Pa) is the pressure exerted when a force of one newton is applied evenly over an area of one square meter.
1Pa=1N/m2
It is a relatively small unit of pressure, so kilopascals (kPa) or megapascals (MPa) are often used in practice.
2. Why is the pascal the standard unit of pressure in the SI system?
Answer:
The pascal in SI units ensures consistency and standardization across scientific and engineering fields. It is derived from base SI units (kg, m, s) and integrates seamlessly with equations involving force, energy, and area, making calculations more coherent and universally interpretable.
3. How do I convert pascal to other pressure units like psi or bar?
Answer:
Here are common conversions:
-
1 bar = 100,000 Pa
-
1 atm = 101,325 Pa
-
1 psi ≈ 6,894.76 Pa
-
1 torr ≈ 133.322 Pa
Example:
Convert 200,000 Pa to psi:
200,000÷6,894.76≈29.0psi
4. What is the difference between pascal, kilopascal, and megapascals?
Answer:
They are scaled versions of the pascal:
-
1 kPa = 1,000 Pa
-
1 MPa = 1,000,000 Pa
These are used for convenience in expressing large pressures:
-
Tire pressure: ~220 kPa
-
Concrete strength: ~25 MPa
5. Why is pascal considered a small unit of pressure?
Answer:
Because 1 Pa represents a very light pressure—approximately the weight of an apple spread over a square meter—it is small in practical terms. That’s why real-world pressures are usually expressed in kPa or MPa.
6. Where is pascal commonly used in daily life?
Answer:
You may encounter pascals in:
-
Tire pressure (e.g., 220 kPa)
-
Weather forecasts (e.g., 1013 hPa = standard atmospheric pressure)
-
Blood pressure machines (internal conversions from mmHg)
-
Air conditioning systems (duct pressures in Pa)
7. Is pascal used in the medical field?
Answer:
Yes. Though blood pressure is typically shown in mmHg, modern medical equipment often uses internal sensors that measure pressure in pascal in SI units for consistency and calibration.
8. Are there different types of pressure measured in pascals?
Answer:
Yes. Pressure can be categorized as:
-
Absolute pressure (relative to a vacuum)
-
Gauge pressure (relative to atmospheric pressure)
-
Differential pressure (difference between two pressure values)
All can be expressed in pascal in SI units.
9. Why is atmospheric pressure usually given in hPa instead of Pa?
Answer:
Since atmospheric pressure at sea level is approximately 101,325 Pa, using hectopascal (hPa) simplifies the value to 1013.25 hPa. This unit is especially common in meteorology.
10. Can I use pascal in SI units with digital sensors and automation systems?
Answer:
Absolutely. Most modern pressure sensors, transducers, and industrial automation systems are designed to measure and output pressure in pascals, kPa, or MPa. This ensures compatibility with other SI-based instruments and software.
11. How is pascal used in physics and engineering calculations?
Answer:
In formulas involving force, area, stress, energy density, and more. For example:
-
Stress:
σ=AF in Pa
-
Pressure energy:
E=P⋅V, where P is in Pa
12. Why was the unit named “pascal”?
Answer:
The unit was named in honor of Blaise Pascal, a French physicist and mathematician who made significant contributions to fluid mechanics and pressure theory, including Pascal’s Law.
XIV. Conclusion
The pascal in SI units stands as one of the most fundamental and universally applied measurements in science, engineering, and everyday life. Defined as one newton of force per square meter, the pascal offers a precise and consistent way to express pressure—an essential quantity that influences everything from weather patterns and fluid flow to mechanical strength and medical monitoring.
Throughout this article, we explored the definition, historical background, and significance of the pascal in SI units, as well as its advantages, common uses, and potential limitations. We also addressed common misconceptions and provided practical conversion methods and examples to illustrate its value across various disciplines.
The beauty of the pascal in SI units lies in its seamless integration with the broader SI framework, allowing it to function effectively alongside other physical quantities like force, area, and stress. Its widespread adoption fosters international collaboration, enhances safety and accuracy in design, and supports innovation in technology and science.
Despite its small base magnitude, the pascal—especially in kilopascals (kPa) and megapascals (MPa)—is a powerful unit that touches nearly every aspect of modern life. Whether you are inflating a tire, designing a skyscraper, analyzing blood pressure, or studying planetary atmospheres, understanding and using the pascal in SI units ensures clarity, precision, and global consistency.
As technology continues to evolve and data becomes increasingly interconnected, the importance of standardized, reliable units like the pascal will only grow. Embracing this SI unit empowers professionals, educators, and learners alike to communicate more effectively and work with greater confidence across borders and disciplines.